Champs d'observation et laboratoire des fictions
Intervention de Rémi Dall'Aglio avec les deuxième année, dans le cadre de l'atelier hybride 2007.
ESPACE DOCUMENTAIRE
MENU
PHYSIQUE
- Lettre au débutant
- Les forces, généralités
- Les 4 forces de la nature
- La grande unification
- Onde électromagnétique
- Tout sur les Unités de mesure
- Acoustique
FORMES
EXPERIENCES
DISPOSITIFS ET MACHINES
Léonard de Vinci , D'Arcy Thompson ,Adrian Bejan, Benoît Mandelbrot, Cantor, Von Koch, Cornu
|
813 . La ramification des plantes.(traité de la peinture) Premièrement : toute branche d'une plante quelconque, si elle n'est pas dominée par son propre poids, s'incurve en élevant son extrémité vers le ciel. Deuxièmement : les rameaux inférieurs qui naissent des branches des arbres sont plus grands que les rameaux supérieurs. Troisièmement : tous les rameaux nés vers le centre de l'arbre dépérissent rapidement, l'ombre y étant excessive. Quatrièmement : les ramifications des plantes seront plus vigoureuses et favorisées si elles sont plus rapprochées des extrémités supérieures de ces plantes, grâce à l'air et au soleil. Cinquièmement : les angles des divisions des ramifications des arbres sont égaux entre eux. Sixièmement : cependant, ces angles se font d'autant plus obtus que les branches qui en forment les côtés vieillissent. Septièmement : le côté d'un de ces angles qui prend le plus d'obliquité est celui qui est constitué du rameau le plus fin. Huitièmement : les rameaux d'une bifurcation, réunis ensemble, recomposent la grosseur de la branche qui leur donne naissance. Par exemple, a et b réunis entre eux donnent e ; e et d réunis entre eux donnent / ; / et e réunis entre eux donnent la grosseur de la branche primitive op, et cette grosseur de op est la somme de toutes les grosseurs a, b, e et d. Il en est ainsi parce que la sève de la branche la plus grosse se divise dans les plus petites. Neuvièmement : il y a autant de courbures des branches maîtresses qu'il y a de naissances de leurs ramifications, qui ne se rencontrent pas entre elles. Dixièmement : la courbure des branches qui se pliera le plus est celle dont les branches ont la grosseur la plus semblable. Ainsi, dans les branches ne et be, qui sont égales entre elles, la branche ned est plus pliée que la ramification aon dont les rameaux sont plus différents. Onzièmement : l'attache de la feuille laisse toujours d'elle-même un vestige au-dessous de son rameau, qui croîtra avec celui-ci jusqu'à ce que l'écorce se fendille et éclate par vieillesse de l'arbre. |
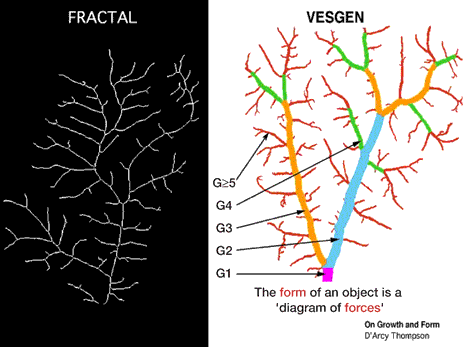
D'Arcy Thompson, la forme et le vivant
Maddalena Mazzocut-Mis
Caractériser le concept de forme, c'est en souligner la complexité intrinsèque. D'un côté, la forme est limite, contour, visibilité d'une surface, aspect mouvant et varié ; de l'autre, c'est la manière dont les parties s'harmonisent dans leur ensemble, coexistent et se structurent. La forme peut être considérée dans son aspect sensible ou être conçue comme idée formelle, impliquant un modèle, un dessin, un type. Quand elle individualise un organisme vivant, la forme est conçue comme structure mobile, comme phénomène changeant et complexe. Cependant, la forme peut aussi être interprétée comme le résultat de l'action de lois physico-chimiques conçues mécaniquement et être ramenée à des déterminations géométriques. Inconnaissable dans sa nature intime, mais identifiable clairement comme effet d'une cause cachée, la forme est définie comme le simple résultat de forces. La morphologie, donc, emprunte sa méthodologie, quoique de façon sélective, à d'autres domaines de recherche.
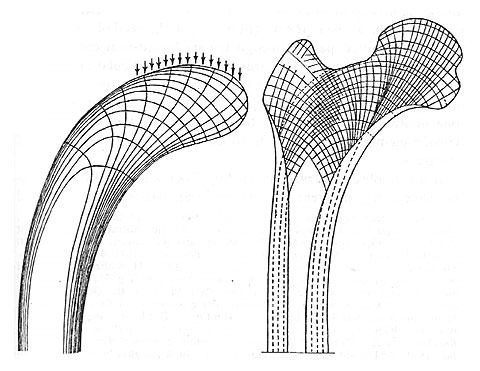
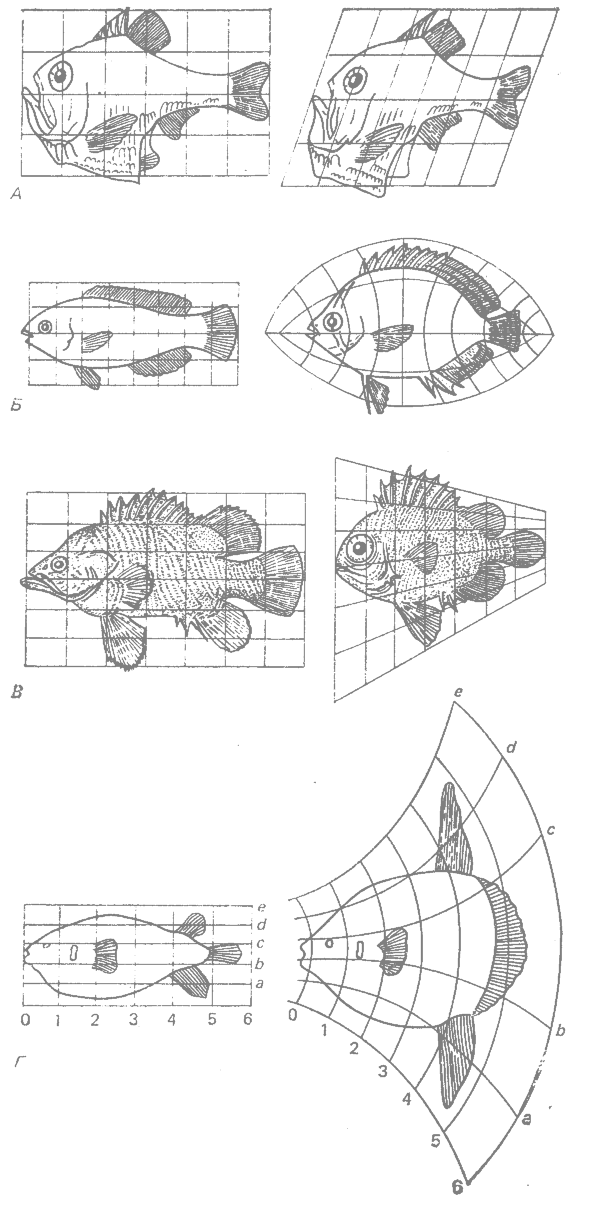
Ce qui précède est, en résumé, la position de D'Arcy Thompson qui, en utilisant un procédé spécial, fournit une identification mathématique et visuelle précise des formes du vivant. Par l'analyse des diverses formes de carapaces des crabes, qui peuvent toutes être ramenées à des déformations successives des coordonnées, initialement orthogonales, d'une seule image ; des formes du squelette des quadrupèdes, qui peuvent être interprétées sur la base de lois de la construction régissant aussi la statique des ponts ; des formes crâniennes de divers animaux, D'Arcy Thompson développe l'idée d'après laquelle la nature s'accroît, se déforme sur la base d'un modèle fort précis. Il existe un logos sous-jacent aux phénomènes, qui ne peut en aucune façon être violé. Les formes de la nature deviennent des objets de la mathématique, étudiés et visualisés avec les instruments classiques de l'analyse géométrique.
La courageuse tentative de D'Arcy Thompson consiste donc à ramener la variété infinie des formes à un schème général, qui soit en mesure de traduire le visible qualitatif en un invisible quantitatif. L'écart qualitatif propre au monde organique est résolu en faveur d'un monde régi par des lois universellement valables. La différenciation morphologique, c'est-à-dire la variété indéfinie des formes, n'éveille chez D'Arcy Thompson aucun sentiment d'émerveillement extasié. C'est plutôt la possibilité de ramener la pluralité morphologique à un procédé régi par un petit nombre de lois formalisables, qui stimule sa recherche solitaire.
La géométrie de l'inerte
Selon la vision de D'Arcy Thompson, la forme du vivant ne représente plus un écart par rapport à la forme inanimée. Toutes deux sont régies par les mêmes lois. Le vivant ne peut plus se targuer de posséder un statut spécial, il doit être expliqué par des lois susceptibles d'être mathématisées.
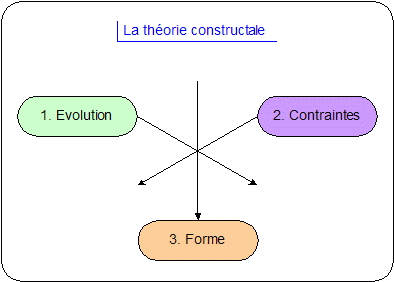
La théorie constructale d'optimisation globale sous des contraintes locales, créée par Adrian Bejan , explique de manière simple l'émergence de nombreuses formes naturelles, en particulier des structures arborescences, telles que les fentes de dessiccation, les méandres de rivières, les poumons, les arbres, ... L'idée constructale est que les architectures de flux naissent d'un principe de maximisation de l'accès aux flux, dans le temps, composée avec leur capacité à se transformer.
Cette théorie permet de concevoir des systèmes optimisés en répartissant au mieux les inévitables résistances internes du système conçu, par exemple un système de refroidissement par fluide caloriporteur, un réseau de distribution d'eau, etc.
Principes
Par exemple, dans les systèmes flux d'un point vers une surface ou d'un point vers un volume, la théorie constructale prévoit des architectures arborescentes, ces flux devant présenter au moins deux régimes résistifs distincts. La théorie s'applique de plus à toutes les échelles : depuis les systèmes microscopiques aux macroscopiques.
| Paquets électroniques | Chaleur | Inserts à haute conductivité | Substrat à faible conductivité |
| Trafic urbain | Personnes | Trafic automobile | Marche dans la structure urbaine |
| Bassins versants | Eau | Ruisseaux et rivières | Flux de Darcy flow dans un milieu poreux |
| Poumons | Air | Voie aériennes et bronches | Diffusion dans les tissus alvéolaires |
| Système sanguin | Sang | Vaisseaux sanguins, capillaires, artères et veines | Diffusion dans les tissus capillaires |
Un principe important de la théorie constructale est de considérer que tous les systèmes sont destinés à demeurer imparfaits du fait de l'existence inévitable de résistances internes (frottements, etc.). D'un point de vue constructal, le mieux que l'on puisse faire est de distribuer de manière optimale ces imperfections, et c'est précisément de cette distribution optimale des imperfections que la forme du système émerge spontanément.
La théorie constructale a été développée par Adrian Bejan, diplômé du MIT et professeur d'ingénierie mécanique à l'université Duke de Caroline du Nord. Elle vise à expliquer l'origine des formes, qui semblent se développer selon des algorithmes comparables dans des domaines très différents (le minéral, le vivant, le sociétal).
Elle se résume de la façon suivante. Dans la nature, la complexité naît de la combinaison de processus élémentaires. Ce sont les lois simples de la physique macroscopique, et plus particulièrement de la thermodynamique, qui génèrent l'apparition des formes. Elles se traduisent par une optimisation destinée à diminuer les dépenses d'énergie et de matière pour lutter au mieux contre l'entropie. Le facteur générateur de cette recherche d'optimisation est l'évolution compétitive pour la survie dans laquelle s'affrontent les divers éléments de la matière et de la vie.

Rarement une notion mathématique aura eu autant de succès auprès de publics divers. La raison en est due en bonne partie au zèle mis par Benoît Mandelbrot , le « père » de cette branche des mathématiques, à la diffuser et par celui de ceux qui ont emboîté ses pas pour l'utiliser dans de très nombreux domaines. En particulier les livres de Mandelbrot « Les objets fractals » et « The fractal geometry of Nature » n'ont pas cessé d'être réédités et ont été lus par un nombre considérable de personnes d'horizons et de cultures très divers. Mais il y a au moins deux autres bonnes raisons : la première est que le concept lui-même a un côté fascinant parce qu'il conduit à une certaine forme d'infini ; la deuxième est qu'il est possible de produire des images étranges et d'une grande beauté en utilisant les mathématiques fractales.
Le mérite de Mandelbrot est d'avoir trouvé ce qu'il y avait de commun à des choses aussi diverses que certaines figures géométriques étranges, la distribution des parasites sur les lignes de transmission de signaux, la longueur des côtes, les cours boursiers, le régime des crues de certains fleuves, le relief terrestre, la distribution des galaxies, la structure des poumons, des travaux mathématiques très théoriques sur la notion de dimension, sur l'itération de polynômes complexes, et beaucoup des choses encore. Mandelbrot a donc abordé toutes sortes de sujets dont beaucoup avaient été étudiés par d'autres, mais il fut le premier à découvrir et analyser théoriquement les lois générales qui les rapprochent.
| Ensemble triadique de Cantor (poussière de Cantor) : |
Il s'agit d'un ensemble d'aspect fractal que Cantor exhiba (1883) montre qu'un ensemble ne contenant aucun intervalle et ayant alors l'apparence d'un ensemble infini dénombrable peut cependant avoir la puissance du continu :

Spirale de Cornu , (1874, Étude sur la diffraction )
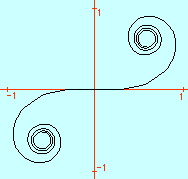

Mécaniquement, la spirale de Cornu est une trajectoire pour laquelle une accélération constante engendre une force centrifuge constante. Ce résultat a son application dans la construction autoroutière (entrée sur une courbe, bretelle de raccordement). En particulier, à vitesse constante ( g = 0), en respectant celle indiquée, en suivant rigoureusement la courbe (pas de coup de volant intempestif...), on doit pouvoir négocier le virage sans problème...
fut le premier à exhiber (1904) à l'étonnement général, une courbe fermée, continue, dérivable en aucun point, sans point double et de périmètre infini pour une aire intérieure finie, confirmant que le concept de courbe, rénové depuis Jordan , mais remis en cause par Cantor et Dedekind , était encore à (re)définir.
Il est facile de construire les premières approches de cette courbe :
- 1- tracez un triangle équilatéral ABC de côté a;
- 2- sur chaque côté, comme [AB], construisez, "au milieu" et à l'extérieur, le triangle équilatéral de côté a/3 et supprimez la base [JK] comme montré ci-dessous;
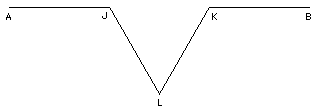
- 3- Réitérer cette construction sur chaque côté des triangles ainsi formés;
- 4- Réitérer indéfiniment la construction sur chaque segment de la figure, ...
 Le périmètre devient infini.Cette courbe ne possède aucun point double (elle ne repasse pas sur elle-même). De périmètre infini, elle possède pourtant une aire intérieure finie (inférieure à celle du cercle circonscrit au triangle initial) !
Le périmètre devient infini.Cette courbe ne possède aucun point double (elle ne repasse pas sur elle-même). De périmètre infini, elle possède pourtant une aire intérieure finie (inférieure à celle du cercle circonscrit au triangle initial) !

